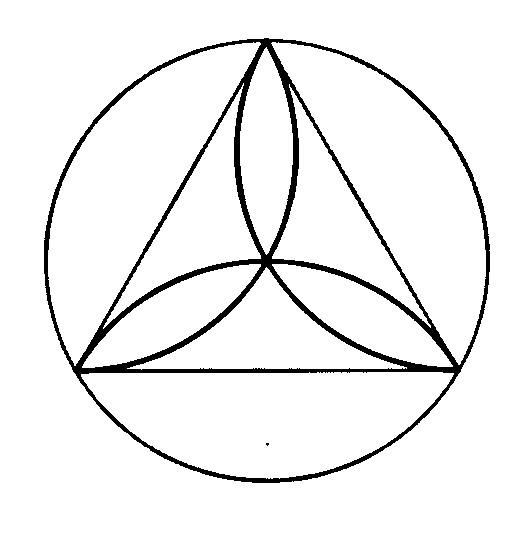
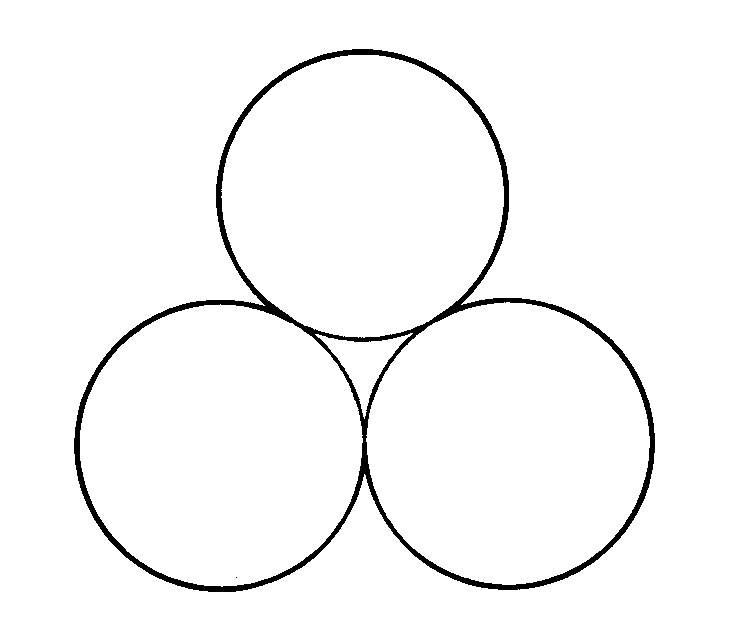
| Curve | Celebri | ||
| Arbelo di Archimede | Salinon | Fuso circolare | Pelecoide |
 |
 |
 |
 |
| Trifoglio | Triangolo curvilineo | Triangolo curvilineo | Lunula |
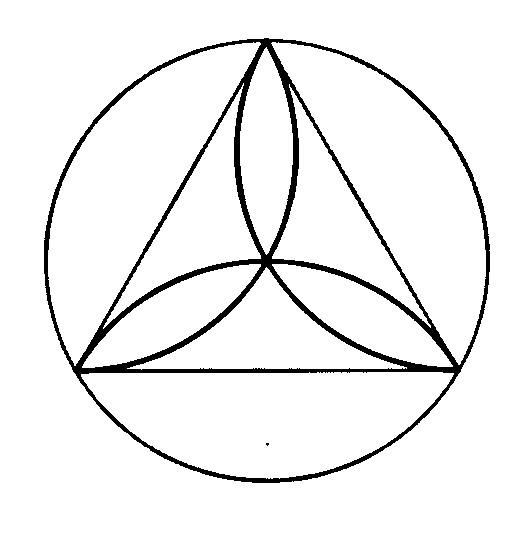 |
 |
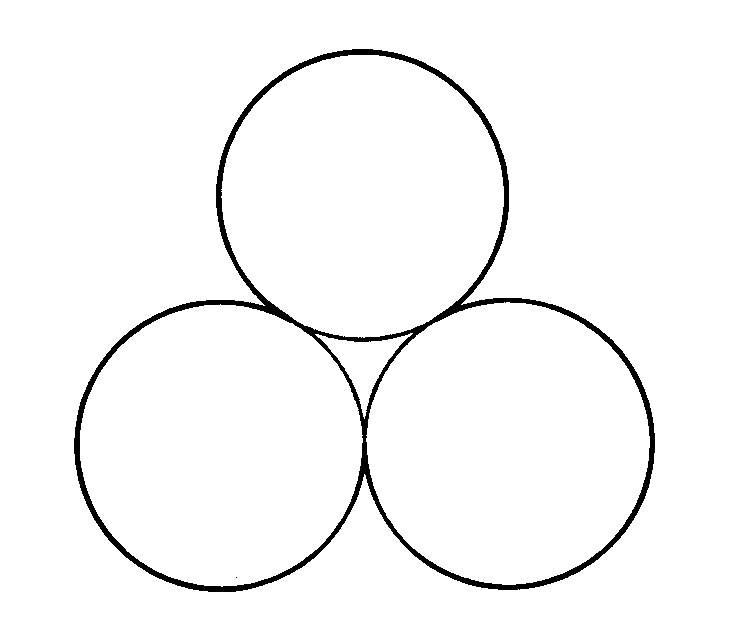 |
 |
| Cicloide | Ellisse | Iperbole | Parabola |

|
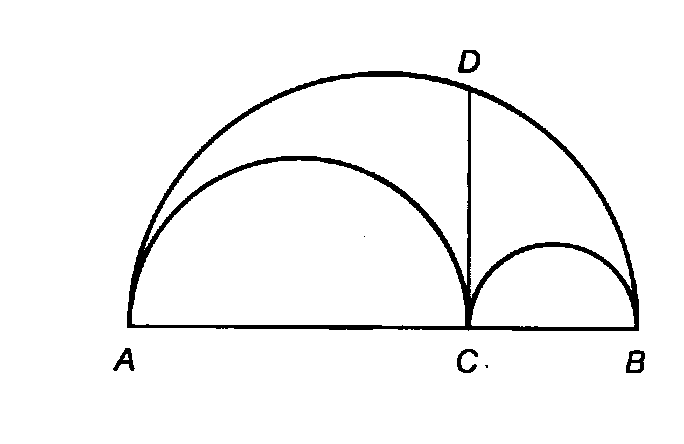
Arbelo di Archimede

E’ la prima figura che
prende il nome da oggetti di uso quotidiano ,in particolare da attrezzi da lavoro
artigianali o contadino. Arbelo è in greco il trincetto da calzolaio.
1)La somma delle tre semicirconferenze è uguale alla circonferenza di diametro AB
pAC/2+pBC/2+pAB/2=pAB
2)L’area
dell’arbelo è uguale all’area del cerchio di diametro CD.
Secondo il
teorema di Euclide CD2=AC·CB
A=pr2 A1=area del semicerchio di diametro AB
A2= area del semicerchio di diametro AC
A3 = area del semicerchio di diametro CB
A1- A2
- A3 =1/2(pAB2/4 - pAC2/4 - pBC2/4)=(p/8)(AB2-AC2-BC2)=(p/8)(AB2-AB2+2CD2)=(p/4)CD2
N.B.:
AC+CB=AB
AC2+BC2=AB2-2AC·CB
AC·BC=CD2
AC2+BC2=AB2-2CD2
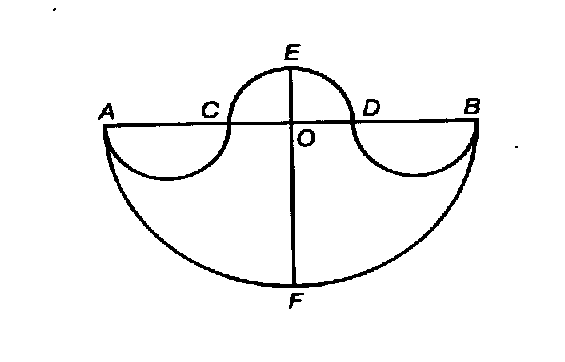
Il Salinon

Sul diametro
AB di un semicerchio si fissano due punti C e
D equidistanti da A e B.
Si tracciano
i semicerchi con diametri AC, CD e DB.
La figura racchiusa dalle quattro
semicirconferenze è la SALIERA:
la sua superficie è equivalente al
cerchio di diametro EF, dove E ed F
sono le intersezioni della perpendicolare in O ad AB
con le due semicirconferenze concentriche.
Perimetro
= Circonferenza di diametro AB
P=p
AB/2+2 p
AC/2+p
CD/2=
= (p/2)(AB+2AC+CD)=
= (p/2)·2 AB=pAB
A=(p/2)·AB2/4+(p/2)(CD2/4)-2(p/2)(AC2/4)=
=(p/8)((2AC+CD)2+CD2-2AC2)=
=(p/8)(4AC2 +CD2+4AC·CD+CD2-2AC2)=
=(p/8)(2AC2+2CD2+4AC·CD)=
=(p/8)2(AC2+CD2+2AC·CD)=
=(p/4)(AC+CD)2=
=(p/4)(AC +CO+OD)2=
=(p/4)(AO+OD)2=
=(p/4)(OF+OE)2=(p/4)EF2
L
PERIMETRO
= 2 ( 1\4 · 2
p L) =
p
L
AREA
= 2 1\4
pL2 –
L2
=
p L2\2 – L2
= L2 (
p\2 –1 )
SOMMA
DI DUE SETTORI CIRCOLARI DI 90°- AREA QUADRATO
In questa figura il fuso
è ricavato da un quadrato, tracciando due archi di circonferenza interni al quadrato, con
centro in due vertici opposti e raggio uguale al lato l del quadrato. L’area dl fuso
circolare si ottiene come differenza tra la somma delle aree dei due settori circolari di
90° (quadranti di cerchio ) e l’area del quadrato stesso.
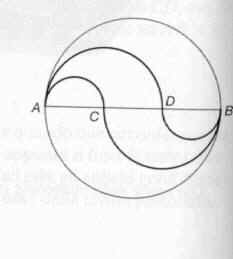
La Pelecoide

Pelecoide significa, in greco, “a forma di
scure”.
Su diametro AB di una circonferenza si fissano due punti qualsiasi
C e D, e si descrivono quattro semicirconferenze con diametri AC, AD, BC e BD, le prime
due e le altre due parti opposte rispetto ad AB. La figura racchiusa da quattro
semicirconferenze è la pelecoide: il suo
perimetro è uguale alla lunghezza della circonferenza data, mentre la sua area sta
all’area del cerchio di diametro AB come CD sta ad AB.
Perimetro = circonferenza di diametro AB
AD2 – AC2
= (AC + CD)2 – AC2
= (AB – AC)2 – AC2=
= (AB – AC + AC)(AB – AC –AC)
= AB·(AB – 2AC)
Trifoglio
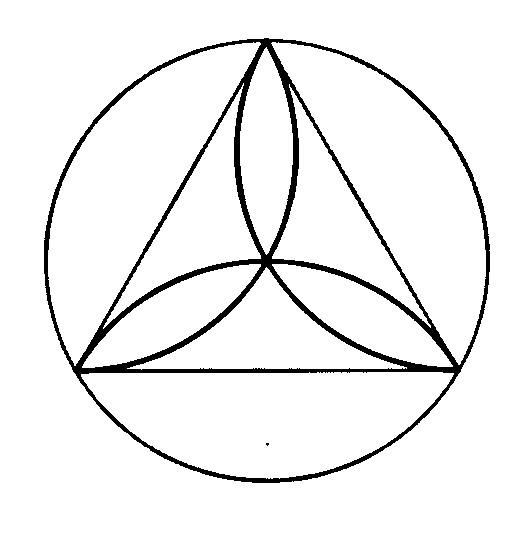
E’ una graziosa figura, costruita partendo da un triangolo equilatero, tracciando i tre archi passanti per il centro del triangolo e per due vertici.
L’area del trifoglio può essere calcolata come differenza tra la somma dei tre settori circolari costruiti sui lati del triangolo, e il triangolo stesso.
DIMOSTRAZIONE:
Perimetro = Circonferenza
di raggio r (OC)
Perimetro = 3 (1/3 · 2 p r) =2 p r
Area = 3 segmenti
circolari - Triangolo ABC
Segmento circolare = 1/3 p r2 -
Triangolo AOB=
=
1/3 p r2 - ½ r/2
rÖ3 =
=(p r2/3)- (r2Ö3/4)=
r2(p/3-Ö3/4)
Area=3 segmenti –
Triangolo ABC=
=3
r2(p/3-Ö3/4) – l2/4 Ö3 =
=3
r2(p/3-Ö3/4) – r2
¾ Ö3=
=3 r2(p/3 - Ö3/4 -
Ö3/4) = 3 r2(p/3-Ö3/2)
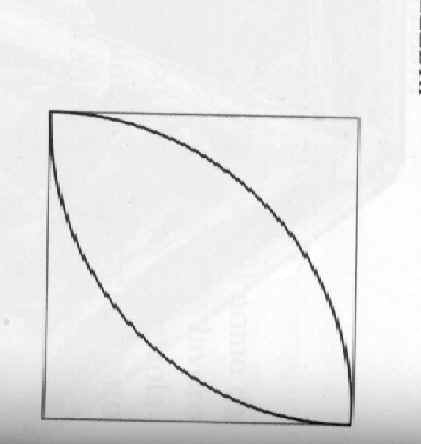
Il triangolo a lati curvilinei

Se abbiamo
tre circonferenze che si toccano esternamente a due a due, si ricava un triangolo a lati
circolari concavi formato dai tre archi minori di ogni circonferenza, compresi tra i punti
di contatto delle altre due.
Area =
triangolo ABC –3 segmenti circolari =
r2/4Ö3-3 [(1/6)pr2 –(r2/4)Ö3] = r2[Ö3/4-p/2+(3/4)Ö3] = r2(Ö3-p/2)
Triangolo a lati curvilinei (i 3 archi maggiori)
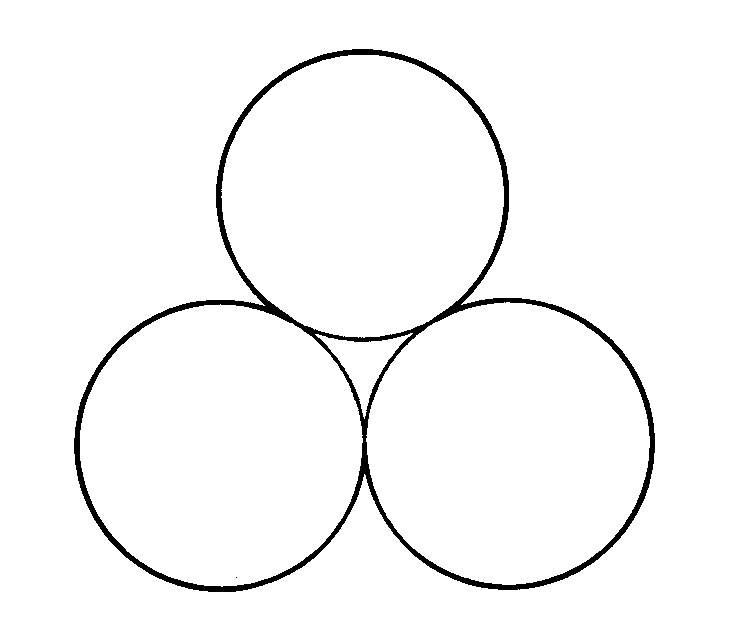
Perimetro =
3·2pr-pr = 5pr
Area = 3pr2+r2(Ö3-p/2) = r2(3p+Ö3-p/2) = r2(5p/2+Ö3).
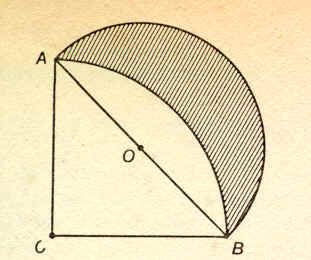
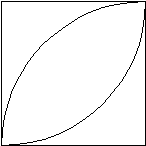
La lunula

La lunula è equivalente alla metà del quadrato di lato l ( o anche al triangolo ABC)
AC = l CB = l AB = lÖ2
PERIMETRO=pl/2 +pl Ö 2/2 = pl
(1+Ö2)/2
1/2 p (l2/2)-[ p
l2/4– l2/2]=
=p l2/4-(p l2/4 - l2/2 )=
=p l2/4 - pl2/4 + l2/2 = l2/2
equivalente alla metà del quadrato di lato l (o al quadrato di lato lÖ 2/2)
Questa è la quadratura
della Lunula
mentre la quadratura del cerchio non è possibile con il solo uso di riga e compasso .
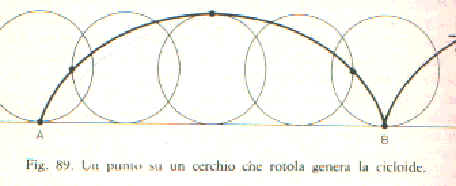

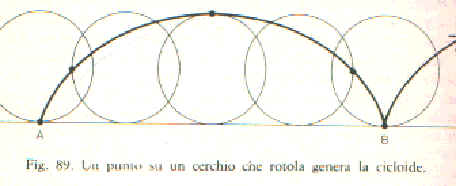
Galileo aveva anche studiato la cicloide. la curva descritta da un punto che si muove su di un cerchio che rotola su di un piano orizzontale e cercò di calcolare l'area racchiusa da un arco di tale curva.
Ma riuscì solo a tracciare la curva sulla carta, ritagliare un arco e di pesarlo , concludendo che era di poco inferiore a 3 volte il cerchio generatore
Detta l'Elena della matematica a causa delle polemiche e controversie che scatenò tra i matematici del tempo . Nel 1615 Mersenne aveva richiamato l'attenzione dei matematici sulla cicloide, forse per averne sentito qualcosa da Galileo suo corrispondente Nel 1628 ne parlò a Roberval che nel 1634 dimostrò che l'area delimitata dall'arco della curva è esattamente 3 volte l'area del cerchio generatore. Roberval non pubblicò le sue scoperte relative alla cicloide (che egli chiamava trocoide (da ruota) )Nel frattempo si era interessato alla cicloide anche Torricelli, forse attraverso Galileo.
Nel 1643 Torricelli inviò a Mersenne la quadratura della cicloide e nel 1644 pubblicò "De parabole" nella cui appendice inserì la quadratura della cicloide.
Nel 1646 Roberval accusò Torricelli di plagio
Oggi è chiaro che la priorità della scoperta spetta a Roberval ma la priorità della pubblicazione va a Torricelli il quale probabilmente rifece indipendentemente la scoperta dell'area.
Inoltre nel 1658 Sir Cristopher Wren fu il primo a dimostrare che la lunghezza della cicloide da cuspide a cuspide è 4 volte il diametro del cerchio generatore .
Le proprietà meccaniche della cicloide sono altrettanto notevoli:
Il pendolo cicloidale (che oscilla tra due rami di cicloide ) descrive una cicloide ed è isocrono( i tempi di oscillazione sono uguali con qualsiasi ampiezza ) (Huygens 1673).
Inoltre la cicloide è tautocrona ( curva di uguali tempi di discesa : qualsiasi sia il punto di partenza di una sfera che cade lungo la curva capovolta , la sfera giungerà sul fondo nello stesso tempo)(Huygens)
E' anche brachistocrona (curva dei minimi tempi ) ossia la cicloide è la curva che congiunge due punti A e B in modo che una sfera posta in A arriva in B lungo la curva nel minimo tempo (Bernoulli 1696)
Alcuni matematici francesi ed italiani mostrarono più tardi che l'area dell'arco era esattamente 3 volte l'area del cerchio generatore.
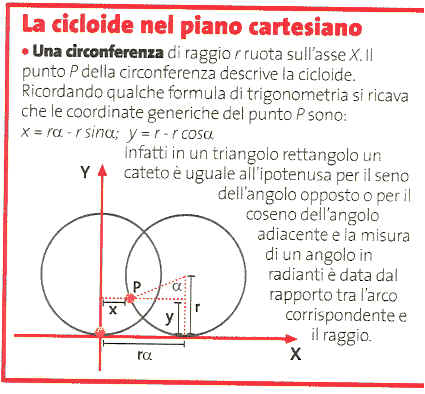


La storia di alcune figure geometriche come ellissi, parabole, circonferenze e iperboli risale alle origini della matematica. Tali figure sono osservabili direttamente in natura. Il primo a scoprirle fu Menecmo, matematico della scuola platonica del IV sec. a.C., che intersecò la superficie di un cono con un piano perpendicolare a une generatrice (semiretta che descrive la superficie di un cono ruotando intorno ad un asse). Osservò che si otteneva una parabola se l’apertura del cono era uguale a 45°, un’ellisse se minore di 45°, un’iperbole se maggiore. L’opera antica più famosa e più completa sull’argomento è Le sezioni coniche di Apollonio di Perga, nato intorno al 262 a.C. Apollonio, a differenza di Menecmo, dimostrò che da un qualunque cono si potevano ottenere tutte e tre le curve, variando l’inclinazione del piano. Inoltre utilizzò, al posto del semplice cono, un cono doppio, tipo clessidra. Con quest’ultima innovazione l’iperbole venne ad essere costituita da due rami. Infatti per ottenere un’iperbole è necessaria un’inclinazione del piano che gli faccia incontrare entrambe le falde del cono. L’attuale linguaggio dell’algebra è stato ideato da René Descartes e Pierre de Fermat (XVII secolo) che tracciarono in un piano due semirette perpendicolari, comunemente chiamate assi X e Y, e individuarono l’esatta posizione di ciascun punto mediante una coppia di numeri detti “coordinate cartesiane”. Ciascuna coordinata esprime la distanza del punto da una degli assi. Per esempio il punto P, che dista 4 unità dall’asse Y e 5 dall’asse X, si indicherà come P=(4,5). Dalla seconda metà del XVII sec., introdotte le coordinate negative, il piano cartesiano sarà definitivamente costituito di quattro quadranti. In questo modo è possibile trasformare qualunque problema geometrico in una relazione algebrica e viceversa. Per esempio un’insieme di punti che hanno le due coordinate uguali (Y=X) formano la retta bisettrice del primo e del terzo quadrante: infatti la bisettrice di un angolo è per definizione l’insieme dei punti equidistanti dai lati dell’angolo dato. Generalizzando: data un’equazione algebrica, cioè un espressione matematica che indica qual è la legge che lega tra loro due quantità, si può trovare sul piano cartesiano la linea che rappresenta l’insieme dei punti con le coordinate che rispettano la legge data dall’equazione. Simmetricamente, data la curva soddisfacente certe condizioni, si può trovare l’equazione corrispondente. Nacque così l’idea di curva come “luogo geometrico”, cioè come insieme di tutti e soli i punti che soddisfano una determinata proprietà. Traducendo i risultati geometrici di Apollonio nell’attuale linguaggio algebrico, possiamo dire che egli trovò l’equazione della parabola nella forma y2 =lx; per qualunque punto si scelga su di essa, il quadrato di lato y ha la stessa area del rettangolo di lati l=4p (costante, dove p è la distanza dal fuoco F dal vertice) e x (variabile); per questo la chiamò parabola, che in greco significa paragone, confronto. Le equazioni dell’ellisse e dell’iperbole sono rispettivamente y2=lx-b2x2/a2 e y2=lx+b2x2/a2 ossia y2 < lx per l’ellisse, che in greco significa mancanza, y2 > lx per l’iperbole, che significa eccedenza.
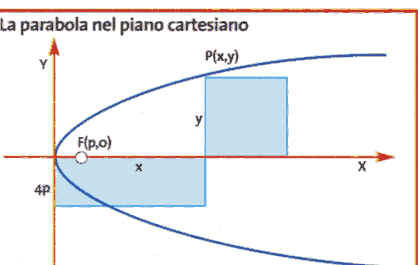

Nel seicento le suddette figure
geometriche furono riprese, liberate dal cono, da alcuni matematici che attribuirono alle
variabili X e Y valori soddisfacenti un’equazione di secondo grado di coefficienti
dati. Variando i coefficienti le coniche variano l’una nell’altra. Nel 1655 John
Wallis tradusse in forma algebrica tutte le proprietà trovate per via geometrica da
Apollonio. Precedentemente Johannes Kepler (1571-1630), elaborando i dati pazientemente
annotati in più di 20 anni dal famoso astronomo Tycho Brahe, suo maestro, aveva scoperto
che le orbite dei pianeti sono ellittiche gli aveva introdotto un punto di vista nuovo,
possiamo dire “dinamico” e assolutamente moderno: la parabola può essere
considerata come un’ ellisse con un fuoco molto, molto lontano, all’infinito,
che poi, quasi “ricomparendo” dall’altra parte, dà origine
all’iperbole. In natura si possono vedere quotidianamente parabole: qualunque
corpo che viene lanciato in aria cade sulla terra seguendo una traiettoria parabolica. Fu
Galilei a enunciare per primo il principio d’indipendenza dei moti, la legge fisica
che determina questo tipo di traiettoria. La parabola descritta da un pallone lanciato
verso l’alto con una certa inclinazione è il risultato della composizione di un moto
rettilineo uniforme orizzontale con un moto uniformemente decelerato verso l’alto e
poi accelerato verso il basso, a causa dell’attrazione gravitazionale. Il calciatore
che vuole fare goal deve calcolare la parabola giusta per fare entrare la palla in rete;
anche lo zampillo di una fontana ha la forma di parabola e le tracce dei fuochi
d’artificio e le foglie molto lunghe delle piante si dispongono ad arco di parabola.


