Nel suo calcolo approssimato del rapporto tra circonferenza di un cerchio e diametro, Archimede diede un'ulteriore prova della sua abilità di calcolo. Partendo dall'esagono regolare inscritto, egli calcolò i perimetri dei poligoni ottenuti raddoppiando successivamente il numero dei lati fino a raggiungere novantasei lati. Il procedimento iterativo da lui usato per questi poligoni si ricollegava a quello che viene talvolta chiamato l'algoritmo archimedeo. Si sviluppa la serie Pn, pn, P2n, p2n, P4n, p2n, ..., dove Pn e pn sono i perimetri dei poligoni regolari di n lati circoscritti ed inscritti. A partire dal terzo termine, si calcola ogni termine in base ai due termini precedenti prendendo alternativamente le loro medie armonica e geometrica. 

In altri termini,                                    

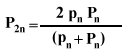
e 

e così via. 
Il suo metodo per calcolare le radici quadrate, per trovare il perimetro dell'esagono circoscritto e per calcolare le medie geometriche era simile a quello usato dai Babilonesi.

Il risultato del calcolo archimedeo relativo alla circonferenza era costituito da un'approssimazione al valore di p espressa dalla disuguaglianza 3(10/71) < p< 3(10/70), che era un valore migliore di quello ottenuto dagli Egiziani e dai Babilonesi (va tenuto presente che né Archimede, né alcun altro matematico greco fece mai uso della nostra notazione p, per indicare il valore del rapporto tra la circonferenza di un cerchio e il suo diametro). Questo risultato viene presentato da Archimede nella Proposizione 3 del trattato Sulla misurazione del cerchio, una delle opere più popolari di Archimede durante il periodo medievale. Questo piccolo trattatello, che è probabilmente incompleto nella forma in cui ci è pervenuto, comprende soltanto tre proposizioni, una delle quali è la dimostrazione, mediante il metodo dell'esaustione, del teorema secondo cui l'area del cerchio è uguale a quella di un triangolo rettangolo che abbia come lati la circonferenza e il raggio del cerchio stesso. E' poco probabile che Archimede sia stato lo scopritore di questo teorema, giacché esso viene presupposto nella quadratura del cerchio attribuita a Dinostrato.