n

n.1

La soluzione dell'enigma n.1

E = Circonferenza dell'equatore

C = Circonferenza del cavo

E = 2p * r

C = 2p * (r + 1)

C -- E = x

2p * (r + 1) - 2p * r = x

2p * [ (r + 1) - r ] = x

2p * ( r + 1 - r ) = x

2p = x

x = 2p (metri)

Pierluigi Conzo

Lucio Salzano

Mirko Di Febbraro

clicca qui per tornare all'inizio

n.2

La soluzione dell'enigma è la seguente:

7 x 7 - (7 + 7) - 7 : 7 - (7 - 7) = 34

49-34=

15 - 14 =

= 1 - 1 == 0 - 0 = 0

clicca qui per tornare all'inizio

n.3

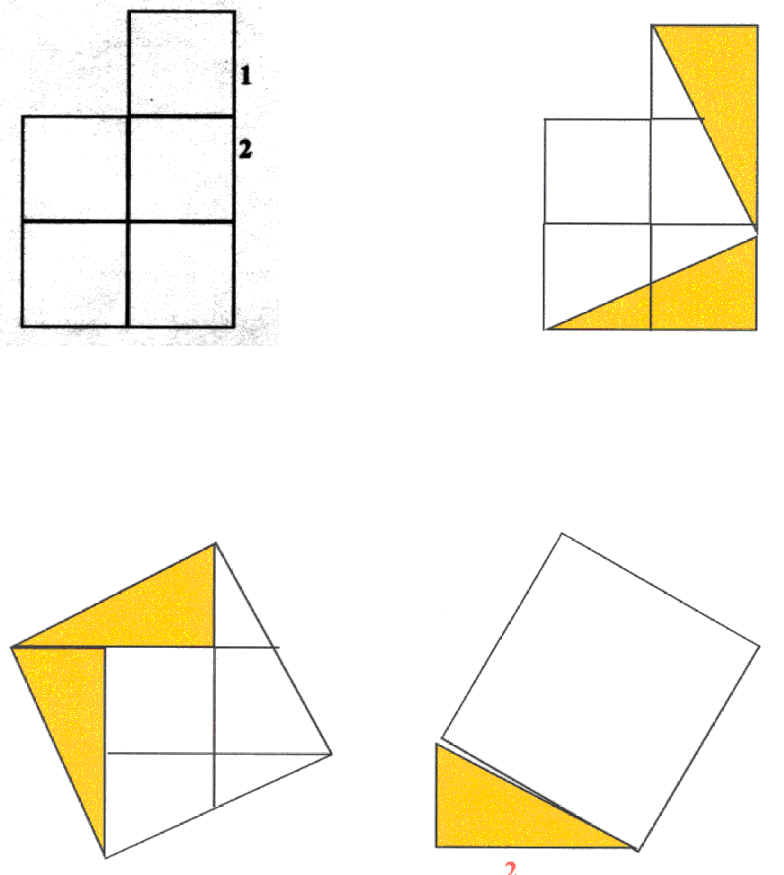
Soluzione enigma n. 3

Costruzione :

Consideriamo 3 circonferenze di raggio r, disposte in modo arbitrario nel piano, siano A,B.C i centri delle circonferenze.

Congiungendo A,B,C si ottiene un triangolo .

Costruire il circocentro O del triangolo (punto di intersezione degli assi del triangolo) .

(asse di un lato del triangolo : perpendicolare per il punto medio del lato)

O è in centro della circonferenza circoscritta al triangolo ,di raggio R=OA=OB=OC

La circonfenza tangente alle 3 circonferenze ha centro in O e raggio R+r.

Se le 3 circonferenze hanno i 3 centri allineati , la circonferenza cercata non esiste.

Image19.gif (3039 byte)

clicca qui per tornare all'inizio

n.4

Soluzione enigma n.4

Per trovare la x dobbiamo scomporre il numero 3, che è uguale alla

3^2. Ma la radice quadrata di 3^2 non è altro che la radice di 9, e questa è

uguale alla radice di 6+3 ( 6+3 ), ma non abbiamo forse già detto che 3 è uguale alla radice quadrata di 3^2?

Anche se può sembrare strano abbiamo risolto l’enigma, infatti possiamo sostituire infinite volte alla radice di 9 la radice di 6+3, e a 3 la radice di 3^2:

quindi x=6

Lucio Salzano 1° A

clicca qui per tornare all'inizio

n.5

Il valore della x è 1

Il ragionamento è il seguente :

X = 1/2 + 1/4 + 1/8 +…

Ogni addendo si divide in due (Es. 1/2 : 2 = 1/4 : 2 = 1/8…) infinite volte, e la loro somma darà sempre l'unità perché…

1= 1/2 + 1/2 sostituiamo…

1 = 1/2 + 1/4 + 1/4 ma…

1 = 1/2 + 1/4 + 1/8 + 1/8 quindi andando nuovamente a sostituire…

1 = 1/2 + 1/4 + 1/8+ 1/16 +1/16 e di nuovo…

1= 1/2+ 1/4 + 1/8+ 1/16 +1/32 +1/32…e così via all'infinito

Pierluigi Conzo 1A

clicca qui per tornare all'inizio

n.6

Soluzione dell’enigma n.6

Occorre dividere la sbarra in 1/40 , 3/40, 9/40 ,27/40 della lunghezza totale in modo che i pesi siano di :

1/40 1 g.

3/40 3 g.

9/40 9 g.

27/40 27 g.

che sono le prime 4 potenze di 3

Con questi pesi distribuiti opportunamente sui 2 bracci della bilancia si può pesare un qualunque oggetto con un peso compreso tra 1g. e 40 g.

clicca qui per tornare all'inizio

n.7

1	2	3	4
8	7	6	5

clicca qui per tornare all'inizio

n.8

Soluzione enigma n.8

Se il professore è nato nel 19xy allora:

89- (10 x +y) = 3(1+9+x+y)

59 = 13 x +4 y

y = (59-13x)/4 l’unica soluzione intera si ha per x=3 e y = 5

89-35 = 54

54 + 10 = 64 età del professore oggi

clicca qui per tornare all'inizio

n.9

Soluzione enigma n.9

Per i numeri pari :

I modi di scegliere le cifre sono:

4(per le centinaia)X3(per le decine) X1(una sola cifra da scegliere il 2)=12

PER IL NUMERO DIVISIBILE PER 5 :

4(per le centinaia) X 3( per le decine) X 1(una sola cifra il 5) = 12

Per il numero dispari:

4(per le centinaia) X 3(per le decine ) X 4 (per le unità tranne il 2) = 48

clicca qui per tornare all'inizio

n.10

Soluzione enigma n.10

In un sacchetto ci sono 30 caramelle di 6 gusti diversi, 5 per ogni gusto. Qual è il numero minimo di caramelle da prendere per averne 2 di gusti diversi e 2 dello stesso gusto?

Se prendiamo 6 caramelle dal sacchetto, anche se cinque di esse dovessero risultare dello stesso gusto, prendendone una sesta si è matematicamente sicuri che tra le caramelle prese ve ne saranno almeno due di gusto diverso.

Prendendo 7 caramelle dal sacchetto, invece, anche se sei di esse dovessero risultare di gusti diversi, prendendone una settima si è matematicamente sicuri che tra le caramelle prese ve ne saranno almeno due dello stesso gusto

Soluzione di:

Conzo Pierluigi

Innangi Michele

Di Febbraro Mirko

Salzano Lucio

clicca qui per tornare all'inizio

N11

Per trovare lo spazio percorso dal gabbiano è necessario sapere lo spazio percorso dalle due navi applicando una proporzione:

V₁ : V₂= S₁ : S₂

25 : 15 = S₁ : S₂

40 : 25 = 80 : x

x = (25 ^.80)/40 = 50

Di conseguenza S₁ = 50 e S₂ = 30

Calcoliamo ora il tempo che impiegano le due navi per incrociarsi:

t = 50/25 = 2h

Possiamo ora calcolare lo spazio percorso dal gabbiano tramite la formula :

S = V*t

S = 30*2

S= 60

Il gabbiano percorre quindi 60 miglia

.Serena Mirra

Pierluigi Conzo

Salzano Lucio

Mirko Di Febbraro

Valentina Mirra

Davide Pecchia

Michele Innangi

I A

clicca qui per tornare all'inizio

n.12

Soluzione enigma .12

Basta disporre i sacchi in fila e prendere una moneta dal primo sacco , due dal secondo , tre dal terzo , quattro dal quarto , cinque dal quinto .

Siccome le monete vere pesano 10 g. il peso di ogni sacco di monete vere sarà sempre un multiplo di 10.

Siccome le monete false pesano 11 g. , la cifra delle unità indicherà il posto del sacco , se la cifra è 1 sarà il primo sacco , se 2 il secondo ecc.

clicca qui per tornare all'inizio

n.13

Soluzione enigma n.13

1 2 6 24 120 .....

1 2 6 24 120 720

infatti :

1X2 =2 X3=6X4=24X5=120X6=720 ecc

Serena e Valentina Mirra 1A

clicca qui per tornare all'inizio

n.14

La soluzione dell'enigma è la seguente:

La povera rana non raggiungerà mai la sua meta in quanto un numero si può dividere all'infinito:

quindi il numero dei salti necessari per raggiungere la meta aggiungendo sempre la metà dello spazio precedente, è di conseguenza infinito !

Conzo Pierluigi

Mirko Di Febbraro

clicca qui per tornare all'inizio

n.15

Enigma n.15

totsol1.jpg (40237 byte)

clicca qui per tornare all'inizio